DPhil student Jonathan Classen-Howes was awarded the Early Career Researcher Poster Prize at the Theory of Condensed Matter Group Meeting organised by IOP at the University of Warwick this summer.
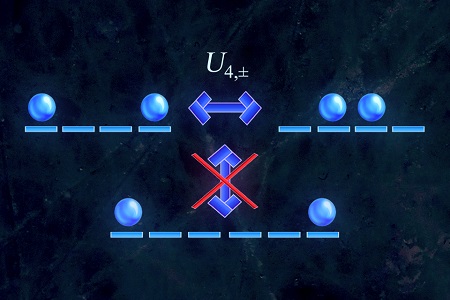
The poster, entitled ‘Phase Transitions in Dipole-Conserving Quantum Spin Systems’, presented on a general class of quantum models of hopping particles on a 1D lattice. These models have applications in such physical contexts as the quantum Hall effect and systems of charged particles exposed to a strong electric field. The particles in the models can be taken to represent spinless fermions, spin excitations, or bosons depending on the context. Interactions between the particles are strictly local, and particle number and centre of mass are conserved. Hence, individual particles cannot propagate independently of each other, leading to ‘fractonic’ dynamics. As a result, quantum states can only evolve to a fraction of the states consistent with their conserved charges.
The poster introduced several new probes for analysing the transition these models undergo from a ‘localised’ phase to a ‘thermalising’ phase. In the localised phase, particles can only propagate within the confines of finite-sized ‘active bubbles’. In the thermalising phase, these active bubbles become extensively large and merge. The poster presented a rigorous lower bound on the critical particle density at which the phase transition occurs and showed through analytic and numerical evidence that this lower bound corresponds to the true critical density. The presentation was based on work done in collaboration with Riccardo Senese and Abhishodh Prakash. Further information can be found in the preprint arXiv: 2408.10321.