Computer simulation has become an indispensable tool for unravelling complicated physical phenomena, particularly those for which reliable experimental data is scarce, or for which an analytical theoretical treatment is impracticable. Nowhere is this more true than in the realm of high-energy-density (HED) physics: warm dense matter, for instance, is notoriously difficult to treat theoretically (due in large part to the comparability of the thermal and Coulomb interaction energies), and is no easier to create or to diagnose in experiment. To overcome these barriers, HED scientists must often appeal to a host of numerical simulation techniques that model the many concurrent processes at play in the HED regime, including atomic kinetics, radiation transfer, hydrodynamics, and laser-plasma interactions.
However, many modern simulations require formidable amounts of computational power to execute. The cost of relatively large-scale atomistic dynamic-compression simulations, for example, is nowadays typically expressed in CPU-years, an expense that even modern supercomputers would struggle to bear routinely. Such severe costs can throttle any prospect of performing an extensive exploration of a simulation's parameter space, or of using simulations to solve the inverse problem, i.e. to identify the set (or sets) of parameters that best explain experimental results.
The cost of performing extremely expensive simulations can in principle be circumvented with the use of an emulator, an algorithm that is taught is recognise the correlation between a simulation's inputs and outputs using judiciously chosen training data, and then to predict what the simulation would yield given new inputs. High-fidelity emulators can thus reproduce the results of a simulation in a tiny fraction of the time by dispensing with its costly internal calculations. The main challenge in realising faithful emulators of this kind is to attain the desired level of accuracy without resorting to using massive training datasets that might be prohibitively expensive to produce (the very problem the emulator is designed to overcome). A recent study led by Muhammad Kasim of the University of Oxford proposes a solution.
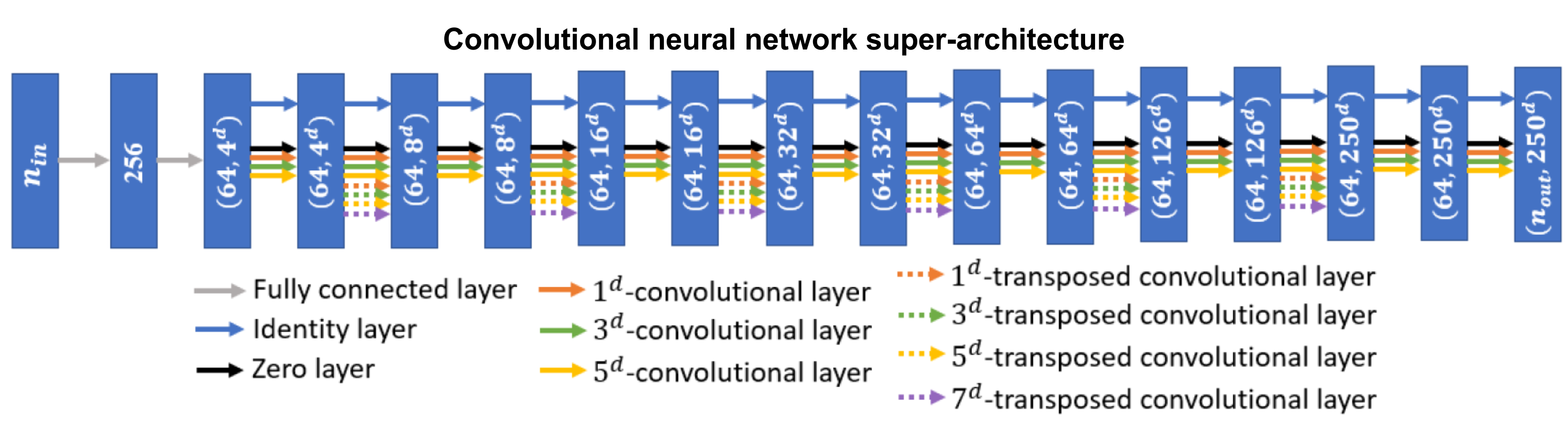
The new technique emulates simulation data using convolutional neural networks, machine-learning systems comprising groups of processing nodes that are densely interconnected via layers of mathematical operations. Ordinarily, the optimal 'wiring' of the network for a given problem is chosen manually. This process is both time-consuming and reliant on subject-specific expertise, and in many cases produces results that are sub-optimal. Kasim et. al. opted instead to automate this optimisation step by first defining a generalised neural network with a novel super-architecture (pictured above), and then iteratively improving its efficiency for the task at hand by varying the connections between computational layers. This method, known as Deep Emulator Network SEarch, or DENSE, allowed the authors simultaneously to identify the particular architecture best-suited for the given simulation and train it to emulate its behaviour.
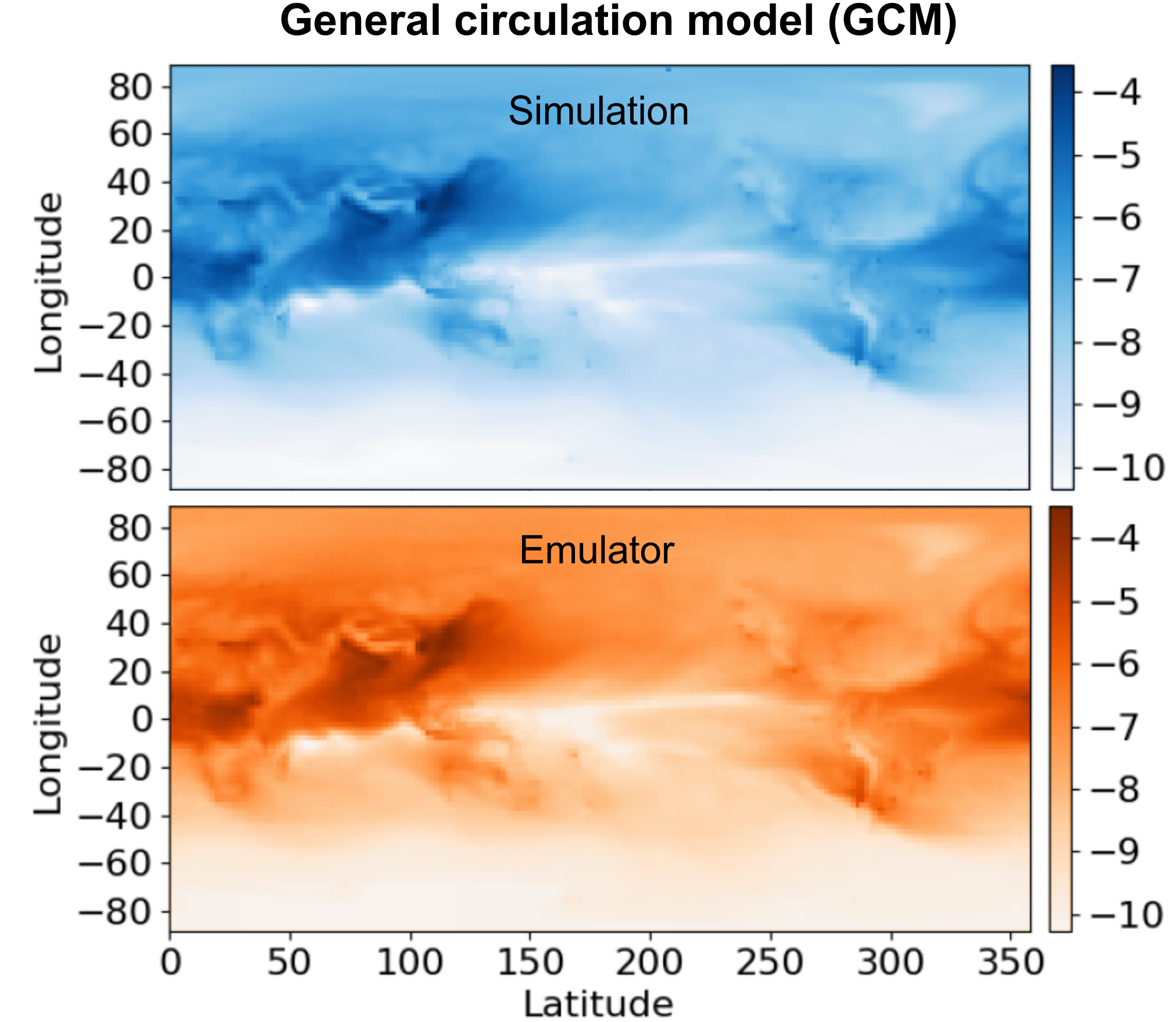
with those of its emulator constructed by DENSE.
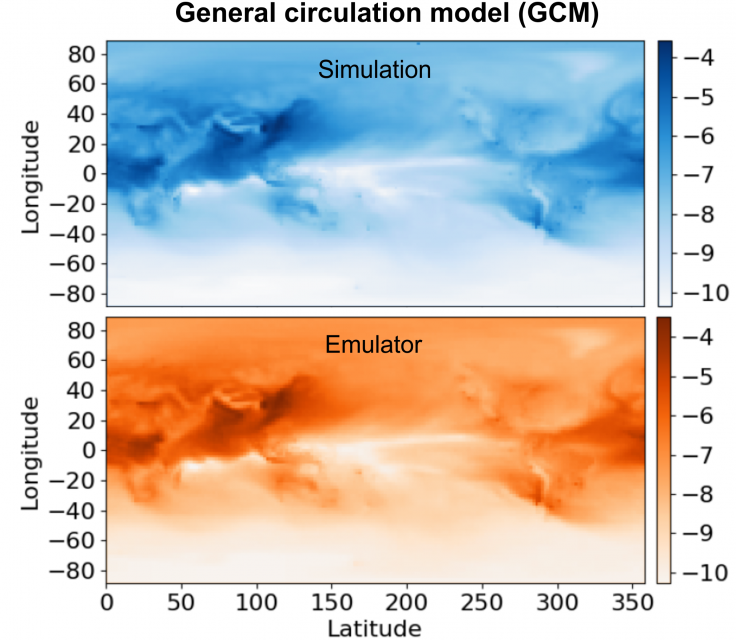
Kasim et. al. applied DENSE to ten disparate scientific simulation cases, including elastic x-ray Thomson scattering (XRTS), seismic tomography, and global climatological modelling. The emulators constructed by DENSE exhibited high accuracy across the board, and in almost every case outperformed non-deep learning techniques and manually constructed deep neural networks by a considerable margin. The emulators were also at least 105 times faster than the simulation they emulated in every instance. In fact, the emulator for the general circulation model (GCM), which simulates the dynamics of aerosol species in the atmosphere, accelerated computation by a factor of over two billion when used with a GPU card - this was despite DENSE having only 39 datapoints with which to train the emulator (due to the prohibitive computational cost of the climate model). A comparison of the simulated and emulated atmospheric data is shown to the right.
The incredible speedup offered by DENSE with even limited training datasets opens up a vista of opportunities in computational analysis and discovery. Inverse problems that would otherwise have been made intractable by a simulation's excessive execution time might become possible. Parameter uncertainty quantification, which is often done via extensive sampling of parameter space via Markov Chain Monte Carlo (MCMC) algorithms and is typically far more expensive that the parameter retrieval itself, could be enabled for computationally intense forward models. It might even become possible to develop advanced online diagnostics capable of retrieving physical parameters from experimental data obtained from HED facilities in real time, allowing scientists to tweak experiments on-the-fly and thus take full advantage of the next generation of high-repetition rate high-power lasers.
An open-access manuscript exhibiting the results of DENSE may be found here.