Theory

Supervisors: Alexander Schekochihin, Michael Barnes

In magnetised astrophysical plasmas, there is a turbulent cascade of electromagnetic fluctuations carrying free energy from large to small scales. The energy is typically extracted from large-scale sources (e.g., in the solar wind, the violent activity in the Sun's corona; in accretion discs, the Keplerian shear flow; in galaxy clusters, outbursts from active galactic nuclei) and deposited into heat---the internal energy of ions and electrons. In order for this dissipation of energy to happen, the energy must reach small scales---in weakly collisional plasmas, these are small scales in the 6D kinetic phase space, i.e., what emerges is large spatial gradients of electric and magnetic fields and large gradients of the particle distribution functions with respect to velocities. This prompts two fundamental questions: (1) how does the energy flow through the 6D phase space and what therefore is the structure of the fluctuations in this space: their spectra, phase-space correlation functions etc. [1,2,3] (these fluctuations are best observed in the solar wind, but we can measure density and magnetic fluctuations even in extragalactic plasmas, via X-ray and radio observations); (2) when turbulent fluctuations are dissipated into particle heat, how is their energy partitioned between various species of particles that populate the plasma: electrons, bulk ions, minority ions, fast non-thermal particles (e.g., cosmic rays) [4,5]. The latter question is particularly important for extragalactic plasmas because all we can observe is radiation from the particles and knowing where the internal energy of each species came from is key to constructing and verifying theories both of turbulence and of macroscale dynamics and thermodynamics. This project has an analytical and a numerical dimension (which of these will dominate depends on the student's inclinations). Analytically, we will work out a theory of phase-space cascade at spatial scales between the ion and electron Larmor scales. Numerically, we will simulate this cascade using "gyrokinetic" equations---an approach in which we average over the Larmor motion and calculate the distribution function of "Larmor rings of charge" rather than particles (this reduces the dimension of phase space to 5D, making theory more tractable and numerics more affordable).

With a theory of plasma turbulence in hand, it is possible to attack what is probably the most fundamental question of the field: in the absence of collisions, are there universal equilibria, or classes of equilibria, independent of initial conditions, that a turbulent plasma will want to converge to? There is some recent progress indicating that the answer is yes and that one can predict statistical-mechanically the emergence of universal power-law (in particle energy) distributions [6]---this is exciting both on its own merits and because of the astrophysical challenge of explaining theoretically power-law distributions that are observed for, e.g., cosmic rays or solar-wind electrons. How to construct a theory of that for a magnetised, turbulent plasma is an open and exciting question. Attempting to do this will again involve kinetic theory and/or kinetic simulations.

Background Reading:

• A. A. Schekochihin et al., "Astrophysical gyrokinetics: kinetic and fluid turbulent cascades in magnetized weakly collisional plasmas," Astrophys. J. Suppl. 182, 310 (2009)
• A. A. Schekochihin et al., "Phase mixing vs. nonlinear advection in drift-kinetic plasma turbulence," J. Plasma Phys. 82, 905820212 (2016)
• R. Meyrand et al., "Fluidization of collisionless plasma turbulence," PNAS 116, 1185 (2019)
• Y. Kawazura et al., "Thermal disequilibration of ions and electrons by collisionless plasma turbulence," PNAS 116, 771 (2019)
• J. Squire et al., "High-frequency heating of the solar wind triggered by low-frequency turbulence," Nature Astron. 6, 715 (2022)
• R. J. Ewart et al., "Relaxation to universal non-Maxwellian equilibria in a collisionless plasma," PNAS 122, e2417813122 (2025); see also A. Schekochihin's MMathPhys Lecture Notes, sec. 10-11

Supervisors: John Magorrian

We now have very good steady-state, axisymmetrized models [1] of the our Galaxy's stars and dark matter content that match observations from Gaia and other catalogues in remarkable detail. Of course, the real Galaxy is neither axisymmetric nor in a steady state: the gravitational potential has contributions from molecular clouds, globular clusters, satellite galaxies, halo substructure and even from the discrete nature of individual stars. Each of these perturbations induces a response in the distribution of the Galaxy's stars and dark matter, "dressed" by its own self gravity, leading to very obvious deviations (e.g., bar, spiral arms) from the baseline steady-state axisymmetric equilibrium models.

The aim of this project is to understand how to use the small deviations between observations and the predictions of these reference axisymmetric models to infer the recent history of the Galaxy's gravitational potential. Previous approaches have relied on an elegant "backward integration" method [2], but this rapidly becomes prohibitively expensive [3] and cannot naturally account for gravitational dressing. In this project we will implement and test a new, more general method that uses perturbation theory [4] to allow whole families of potentials to be considered at once, accounting self-consistently for gravitational dressing. By applying it to our own Galactic disc, we will construct a new, independent map of the disc's stellar (and dark matter) content (a "top-down" view of the Galaxy), and constrain the dynamical mechanisms that drive the spiral structure and the response to the bar.

References:

• [1] Binney & Vasiliev, 2023, MNRAS 520 1832 https://ui.adsabs.harvard.edu/abs/2023MNRAS.520.1832B/abstract
• [2] Dehnen, 2000, AJ 119 800 https://iopscience.iop.org/article/10.1086/301226
• [3] Khalil et al, 2025, A&A 699 A263 https://ui.adsabs.harvard.edu/abs/2025A%26A...699A.263K/abstract
• [4] Magorrian, Galactic & Planetary Dynamics, ch.8 https://www-thphys.physics.ox.ac.uk/people/JohnMagorrian/cm21/cm21.pdf

Supervisors: Archie Bott, Gianluca Gregori, Alexander Schekochihin

There are a number of possibilities within this project to design, take part in, and theorise about laboratory experiments employing laser-produced plasmas to model astrophysical phenomena and basic, fundamental physical processes in turbulent plasmas. Recent examples of our work in this field include turbulent generation of magnetic fields ("dynamo") [1,2], supersonic turbulence mimicking star-forming molecular clouds [3], diffusion and acceleration of particles by turbulence [4,5], suppression of thermal conduction in galaxy-cluster-like plasmas [6]. Our group has access to several laser facilities (including the National Ignition Facility, the largest laser system in the world). Students will also have access to a laser laboratory on campus, where initial experiments can be fielded. Depending on the student's inclinations, it is also possible to pursue a project focused on theory and/or numerical modelling of plasma phenomena in astrophysical and laboratory-astrophysical environments.

References:

• P. Tzeferacos et al., "Laboratory evidence of dynamo amplification of magnetic fields in a turbulent plasma," Nature Comm. 9, 591 (2018) (2019 APS Dawson Prize)
• A. F. A. Bott et al., "Time-resolved fast turbulent dynamo in a laser plasma," PNAS 118, e2015729118 (2021) (2020 EPS PhD Award in Plasma Physics)
• T. G. White et al.,"Supersonic plasma turbulence in the laboratory," Nature Comm. 10, 1758 (2019)
• A. F. A. Bott et al., "Proton imaging of stochastic magnetic fields," J. Plasma Phys. 83, 905830614 (2017)
• L. E. Chen et al., "Transport of high-energy charged particles through spatially intermittent turbulent magnetic fields," Astrophys. J. 892, 114 (2020)
• J. Meinecke et al., "Strong suppression of heat conduction in a laboratory analogue of galaxy-cluster turbulent plasma," Science Adv. 8, eabj6799 (2022)

Supervisors: Gianluca Gregori, Subir Sarkar, Dmitri Uzdensky

Gamma-ray bursts (GRBs) are among the most energetic events in the Universe. They occur at cosmological distances and are the result of the collapse of massive stars or neutron stars mergers, with emission of relativistic "fireballs" of electron-positron pairs. From astrophysical observations, a wealth of information has been gleaned about the mechanism that leads to such strong emission of radiation, with leading models predicting that this is due to the disruption of the beam as it blasts through the surrounding plasma. This produces shocks and hydromagnetic turbulence that generate synchrotron emission, potentially accelerating to ultra-high energies the protons which are observed on Earth as cosmic rays. However, there is no direct evidence of the generation of either magnetic fields or cosmic rays by GRBs. Estimates are often based on crude energy equipartition arguments or idealized numerical simulations that struggle to capture the extreme plasma conditions. We propose to address this lacuna by conducting laboratory experiments at accelerator facilities to mimic the jet propagation through its surrounding plasma. Our intial work [1] has demonstrated that we can create enormous beams of electron-positron plasmas that have properties very similar to GRB Fireballs. We are now planning new experiments at CERN as well as at Laboratori Nazionali Frascati (INFN, Italy) to fully characterize the interaction of these beams with a surrounding (ambient) plasma. Such experiments will enable in-situ measurement of the plasma properties, with exquisite details that cannot be achieved elsewhere. The experiments also complement numerical simulations by providing long measurement times extending into the non-linear regime where numerical simulations are not possible today. The proposed experiments will study fundamental physics processes, unveil the microphysics of GRBs, and provide a new window in high energy astrophysics using novel Earth-based laboratory tools.

Background Reading:

• C. D. Arrowsmith et al., "Laboratory realisation of relativistic pair-plasma beams," Nature Comm. 15, 5029 (2024)

Supervisors: Pedro Ferreira

One of the open question in cosmology is what is driving the accelerated expansion of the Universe? The current belief is that it is some form of energy which in invisible, i.e. it is dark. Recent observations seem to find that simplest proposal, the cosmological constant, doesn't quite explain what we see. On the other hand, the simplest explanations, such as quintessence, seem to not fare much better. The purpose of this project is to get a firm and complete understanding of what we can actually say about the nature of dark energy with current and future observational data. We will build on my recent work with William Wolf and Carlos Garcia Garcia, systematically exploring what microphysical models may be responsible for what we are seeing.

Supervisors: Julien Devriendt, Adrianne Slyz

Low density gas streams along networks of filaments in the intergalactic medium (IGM) until it is funnelled through the circum-galactic medium (CGM). This latter then feeds galaxy growth by replenishing their fuel supply, allowing star formation to proceed deep into the interstellar medium (ISM). In doing so, it mixes with gas ejected by supernovae, stellar winds, and supermassive black hole jets. Most observational studies rely on detecting the CGM in absorption along the line of sights of bright quasars located behind the host galaxy or by looking at the host galaxy itself down-the-barrel. As a result, each observation is limited to one sightline per galaxy, and although statistical studies have yielded some information, they still only hint at the characteristics of the CGM. However, a new generation of instruments is preparing to detect the CGM in emission. This groundbreaking step will allow the direct mapping of extended gaseous haloes around galaxies, leading to measurements of the amount of CGM gas in different phases, their cooling times, and thus, ultimately, their fate.

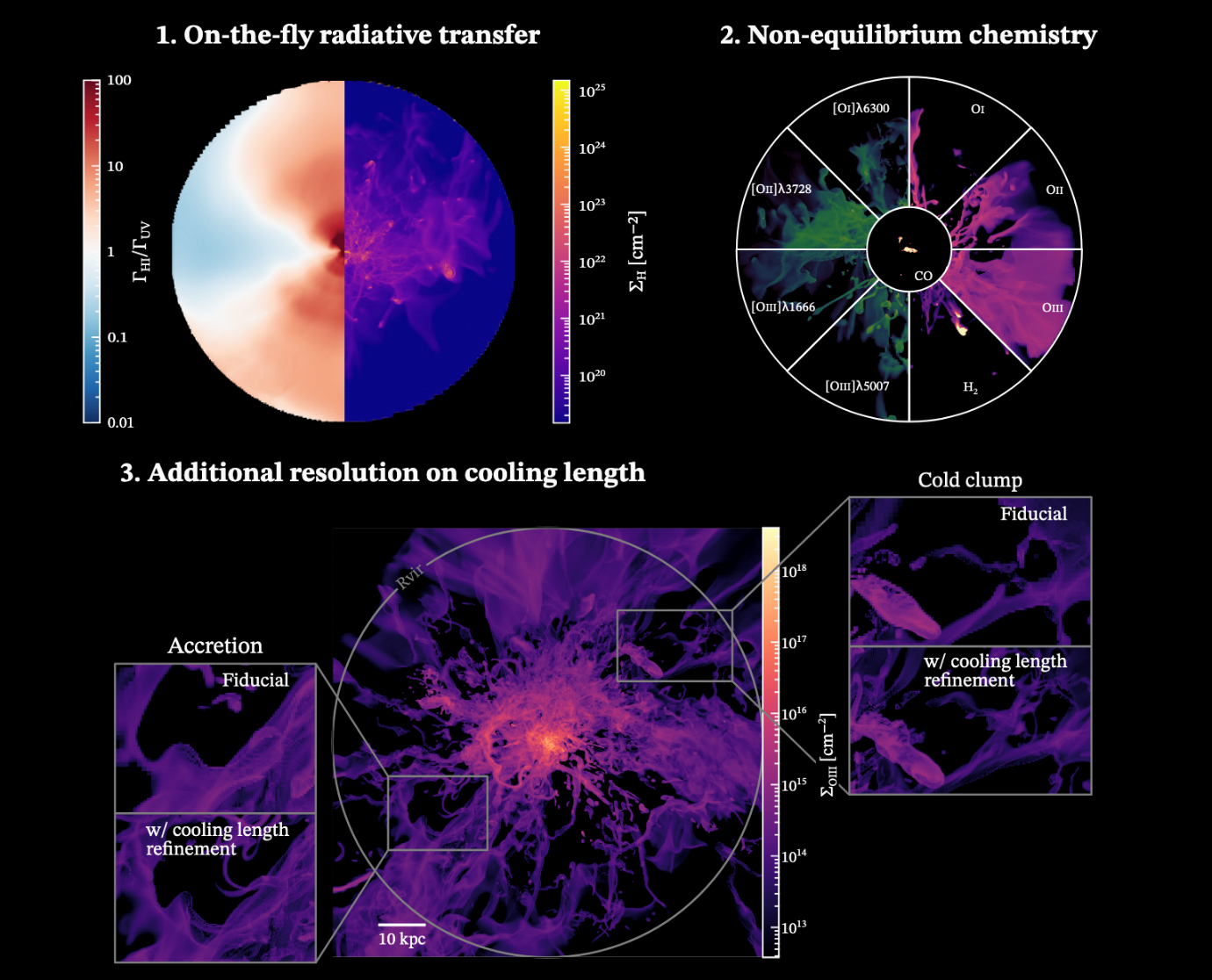
For this project, the DPhil student will perform numerical studies of the CGM within the explicit framework of a cold dark matter dominated Universe, using the adaptive mesh refinement hydrodynamics code RAMSES-RTZ (Katz 2022). This code couples a complex non-equilibrium chemical network to radiative transfer, making it one of the only ones in the world capable to accurately predict emission from the CGM. Such theoretical work is crucial to motivate observations particularly because the CGM gas is low density and thus notoriously difficult to detect. Starting with the MEGATRON suite of cosmological simulations (see references below) performed with RAMSES-RTZ and including tracer particles to follow the Lagrangian evolution of fluid parcels, the student will analyse the CGM emission of high redshift galaxies, looking to understand its dynamics and properties as a function of star formation, environment, etc. In a second stage, they will move on to designing and running their own high-resolution simulations of galaxy formation, adding supermassive black holes, and/or magnetic fields, and/or cosmic rays, components which are missing from the original MEGATRON simulations. Scientific goals include assessing which combinations of emission lines best trace the spatial distribution of the multi-phase CGM at different redshifts, determining distances out to which there is detectable CGM emission and through which lines, pinning down the origin of dense gas in the CGM (inflow or outflow?), and, more generally, shedding light on how the CGM of different galaxies interfaces both with the IGM and ISM on larger and smaller scales respectively.

The DPhil student will be part of an international collaboration (US, France, South Korea, UK) developing and exploiting state-of-the-art, high-resolution, and physics rich cosmological simulations.

References:

• Cadiou et al., “MEGATRON: The impact of non-equilibrium effects and local radiation fields on the circum-galactic medium at cosmic noon”,  arXiv:2510.05667
• Choustikov et al., “MEGATRON: Disentangling physical processes and observational bias in the multi-phase ISM of high redshift galaxies”, arXiv:2510.06347
• Katz et al., “MEGATRON: Reproducing the diversity of high redshift galaxy spectra with cosmological radiation hydrodynamics simulations”, arXiv:2510.05201
• Katz, H. “RAMSES-RTZ: non-equilibrium metal chemistry and cooling coupled to on-the-fly radiation hydrodynamics”, 2022, MNRAS, 512, 348
• Rodriguez Montero, F. et al., 2024, The impact of cosmic rays on the interstellar medium and galactic outflow of Milky Way analogues”, MNRAS, 530, 3617
• Vargas et al., 2025, “Pioneering far UV emission mapping of the circumgalactic medium with Aspera—motivation, mission status, and lessons learned”, Journal of Astronomical Telescopes, Instruments, and Systems, 11, 4, 042216