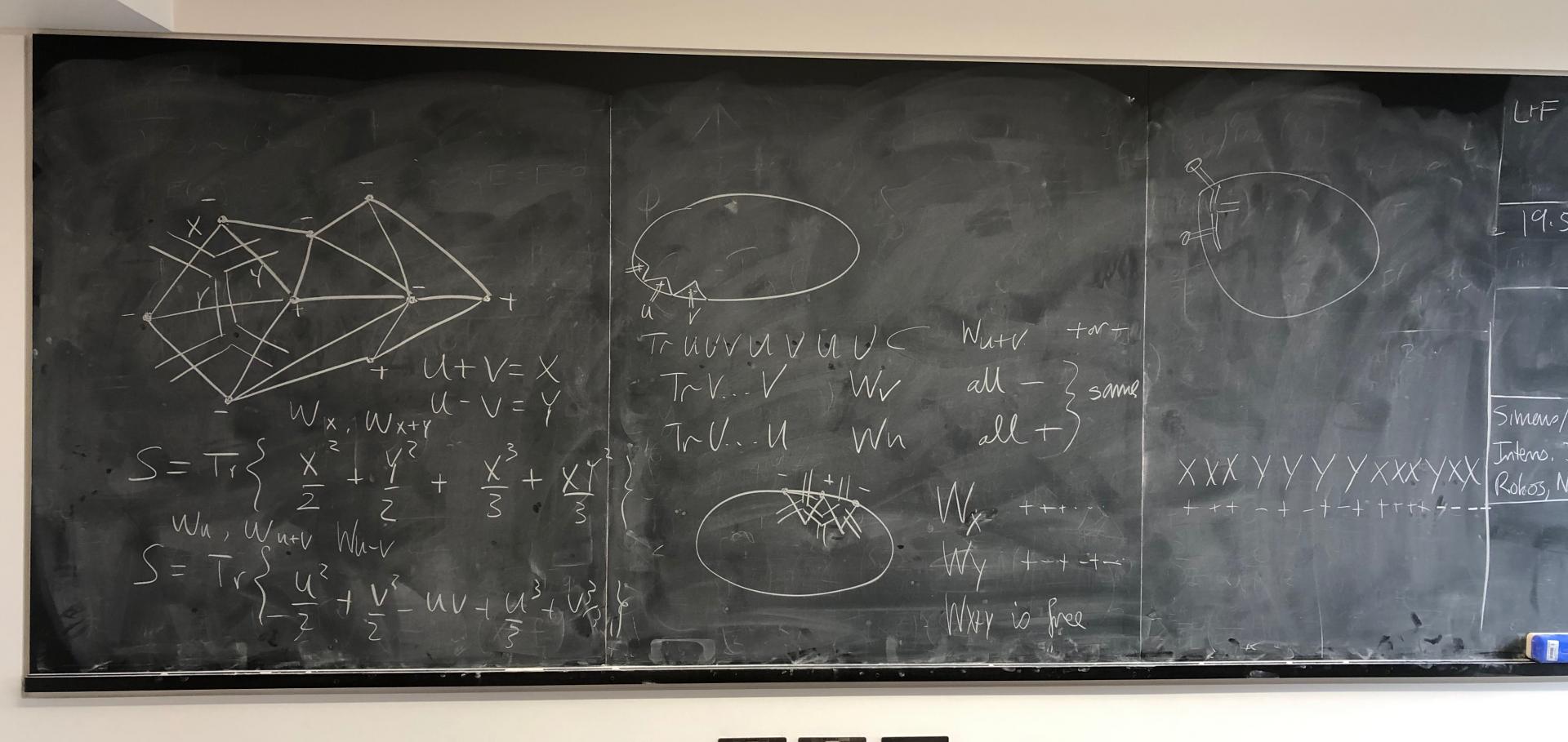John Wheater

Abstract:

We show that the conformal data of a range of large-N CFTs, the melonic CFTs, are specified by constrained extremization of the universal part of the sphere free energy F = − log ZSd, called F~. This family includes the generalized SYK models, the vector models (O(N), Gross-Neveu, etc.), and the tensor field theories. The known F and a-maximization procedures in SCFTs are therefore extended to these non-supersymmetric CFTs in continuous d. We establish our result using the two-particle irreducible (2PI) effective action, and, equivalently, by Feynman diagram resummation. The universal part of F~ interpolates in continuous dimension between the known C-functions, so we can interpret this result as an extremization of the number of IR degrees of freedom, in the spirit of the generalized c, F, a-theorems. The outcome is a complete classification of the melonic CFTs: they are the conformal mean field theories which extremize the universal part of the sphere free energy, subject to an IR marginality condition on the interaction Lagrangian.

Abstract:

We study a set of large-N tensor field theories with a rich structure of fixed points, encompassing both the melonic and prismatic CFTs observed previously in the conformal limits of other tensor theories and in the generalised Sachdev-Ye-Kitaev (SYK) model. The tensor fields interact via an O(N) 3 -invariant generalisation of the quartic Yukawa model, ϕ 2ψψ¯ +ϕ 6 . To understand the structure of IR/UV fixed points, we perform a partial four-loop perturbative analysis in D = 3 − ϵ. We identify the flows between the melonic and prismatic fixed points in the bosonic and fermionic sectors, finding an apparent line of fixed points in both. We reproduce these fixed points non-perturbatively using the Schwinger-Dyson equations, and in addition identify the supersymmetric fixed points in general dimension. Selecting a particular fermionic fixed point, we study its conformal spectrum non-perturbatively, comparing it to the sextic prismatic model. In particular, we establish the dimensional windows in which this theory remains stable. We comment on the structure of large-N melonic CFTs across various dimensions, noting a number of features which we expect to be common to any such theory.